Greedy Algorithms in DAA

Greedy Introduction

Greedy algorithms are simple and straightforward. They are shortsighted in their approach in the sense that they take decisions on the basis of information at hand without worrying about the effect these decisions may have in the future. They are easy to invent, easy to implement and most of the time quite efficient. Many problems cannot be solved correctly by greedy approach. Greedy algorithms are used to solve optimization problems

Greedy Approach

Greedy Algorithm works by making the decision that seems most promising at any moment; it never reconsiders this decision, whatever situation may arise later.

As an example consider the problem of "Making Change".

Coins available are:

• dollars (100 cents)
• quarters (25 cents)
• dimes (10 cents)
• nickels (5 cents)
• pennies (1 cent)

Problem    Make a change of a given amount using the smallest possible number of coins.

• Start with nothing.
• at every stage without passing the given amount.
  • add the largest to the coins already chosen.

Make change for n units using the least possible number of coins.
MAKE-CHANGE (n)
        C ← {100, 25, 10, 5, 1}     // constant.
        Sol ← {};                         // set that will hold the solution set.
        Sum ← 0 sum of item in solution set
        WHILE sum not = n
            x = largest item in set C such that sum + x ≤ n
            IF no such item THEN
                RETURN    "No Solution"
            S ← S {value of x}
            sum ← sum + x
        RETURN S

Example     Make a change for 2.89 (289 cents) here n = 2.89 and the solution contains 2 dollars, 3 quarters, 1 dime and 4 pennies. The algorithm is greedy because at every stage it chooses the largest coin without worrying about the consequences. Moreover, it never changes its mind in the sense that once a coin has been included in the solution set, it remains there.


To construct the solution in an optimal way. Algorithm maintains two sets. One contains chosen items and the other contains rejected items.
The greedy algorithm consists of four (4) function.

1. A function that checks whether chosen set of items provide a solution.
2. A function that checks the feasibility of a set.
3. The selection function tells which of the candidates is the most promising.
4. An objective function, which does not appear explicitly, gives the value of a solution.

• Initially the set of chosen items is empty i.e., solution set.
• At each step
  • item will be added in a solution set by using selection function.
  • IF the set would no longer be feasible
    • reject items under consideration (and is never consider again).
  • ELSE IF set is still feasible THEN
    • add the current item.

 

Definitions of feasibility

A feasible set (of candidates) is promising if it can be extended to produce not merely a solution, but an optimal solution to the problem. In particular, the empty set is always promising why? (because an optimal solution always exists)

Unlike Dynamic Programming, which solves the subproblems bottom-up, a greedy strategy usually progresses in a top-down fashion, making one greedy choice after another, reducing each problem to a smaller one. 
The "greedy-choice property" and "optimal substructure" are two ingredients in the problem that lend to a greedy strategy.
It says that a globally optimal solution can be arrived at by making a locally optimal choice.

 

Knapsack Problem

Statement    A thief robbing a store and can carry a maximal weight of w into their knapsack. There are n items and i^th  item weigh w_i and is worth v_i dollars. What items should thief take?

There are two versions of problem

1. Fractional knapsack problemThe setup is same, but the thief can take fractions of items, meaning that the items can be broken into smaller pieces so that thief may decide to carry only a fraction of x_i of item i, where 0 ≤ x_i ≤ 1.
   Exhibit greedy choice property.
   • Greedy algorithm exists.
   Exhibit optimal substructure property.
   • ?????
2. 0-1 knapsack problemThe setup is the same, but the items may not be broken into smaller pieces, so thief may decide either to take an item or to leave it (binary choice), but may not take a fraction of an item.
   Exhibit No greedy choice property.
   • No greedy algorithm exists.
   Exhibit optimal substructure property.
   • Only dynamic programming algorithm exists.

 

Dynamic-Programming Solution

to the 0-1 Knapsack Problem

Let i be the highest-numbered item in an optimal solution S for W pounds. Then S`= S - {i} is an optimal solution for W-w_i pounds and the value to the solution S isV_i plus the value of the subproblem.

We can express this fact in the following formula: define c[i, w] to be the solution for items  1,2, . . . , i and maximum weight w. Then

	0	if i = 0 or w = 0
c[i,w]  =	c[i-1, w]	if wi ≥ 0
	max [vi + c[i-1, w-wi], c[i-1, w]}	if i>0 and w ≥ wi

This says that the value of the solution to i items either include i^th item, in which case it is v_i plus a subproblem solution for (i-1) items and the weight excluding w_i, or does not include i^th item, in which case it is a subproblem's solution for (i-1) items and the same weight. That is, if the thief picks item i, thief takes v_i value, and thief can choose from items w-w_i, and get c[i-1, w-w_i] additional value. On other hand, if thief decides not to take item i, thief can choose from item 1,2, . . . , i-1 upto the weight limit w, and get c[i-1, w] value. The better of these two choices should be made.
Although the 0-1 knapsack problem, the above formula for c is similar to LCS formula: boundary values are 0, and other values are computed from the input and "earlier" values of c. So the 0-1 knapsack algorithm is like the LCS-length algorithm given in CLR-book for finding a longest common subsequence of two sequences.
The algorithm takes as input the maximum weight W, the number of items n, and the two sequences v = <v₁, v₂, . . . , v_n> and w = <w₁, w_2, . . . , w_n>. It stores the c[i, j] values in the table, that is, a two dimensional array, c[0 . . n, 0 . . w] whose entries are computed in a row-major order. That is, the first row of c is filled in from left to right, then the second row, and so on. At the end of the computation, c[n, w] contains the maximum value that can be picked into the knapsack.

Dynamic-0-1-knapsack (v, w, n, W)

for w = 0 to W
    do c[0, w] = 0
for i = 1 to n
    do c[i, 0] = 0
        for w = 1 to W
            do if w_i ≤ w
                 then if v_i + c[i-1, w-w_i]
                       then c[i, w] = v_i + c[i-1, w-w_i]
                       else c[i, w] = c[i-1, w]
                 else
                      c[i, w] = c[i-1, w]

The set of items to take can be deduced from the table, starting at c[n. w] and tracing backwards where the optimal values came from. If c[i, w] = c[i-1, w] item i is not part of the solution, and we are continue tracing with c[i-1, w]. Otherwise item i is part of the solution, and we continue tracing with c[i-1, w-W].

Analysis
This dynamic-0-1-kanpsack algorithm takes θ(nw) times, broken up as follows:
θ(nw) times to fill the c-table, which has (n+1).(w+1) entries, each requiring θ(1) time to compute. O(n) time to trace the solution, because the tracing process starts in row n of the table and moves up 1 row at each step.

 

Greedy Solution to the

Fractional Knapsack Problem

 

There are n items in a store. For i =1,2, . . . , n, item i has weight w_i > 0 and worth v_i > 0. Thief can carry a maximum weight of W pounds in a knapsack. In this version of a problem the items can be broken into smaller piece, so the thief may decide to carry only a fraction x_i of object i, where 0 ≤ x_i ≤ 1. Item i contributes x_iw_ito the total weight in the knapsack, and x_iv_i to the value of the load.
In Symbol, the fraction knapsack problem can be stated as follows.
maximize ⁿS_i=1 x_iv_i subject to constraint ⁿS_i=1 x_iw_i ≤ W
It is clear that an optimal solution must fill the knapsack exactly, for otherwise we could add a fraction of one of the remaining objects and increase the value of the load. Thus in an optimal solution ⁿS_i=1 x_iw_i = W.

Greedy-fractional-knapsack (w, v, W)

FOR i =1 to n
    do x[i] =0
weight = 0
while weight < W
    do i = best remaining item
        IF weight + w[i] ≤ W
            then x[i] = 1
                weight = weight + w[i]
            else
                x[i] = (w - weight) / w[i]
                weight = W
return x

Analysis  
If the items are already sorted into decreasing order of v_i / w_i, then
            the while-loop takes a time in O(n);
Therefore, the total time including the sort is in O(n log n).

If we keep the items in heap with largest v_i/w_i at the root. Then

• creating the heap takes O(n) time
• while-loop now takes O(log n) time (since heap property must be restored after the removal of root)
   

Although this data structure does not alter the worst-case, it may be faster if only a small number of items are need to fill the knapsack.

One variant of the 0-1 knapsack problem is when order of items are sorted by increasing weight is the same as their order when sorted by decreasing value.
The optimal solution to this problem is to sort by the value of the item in decreasing order. Then pick up the most valuable item which also has a least weight. First, if its weight is less than the total weight that can be carried. Then deduct the total weight that can be carried by the weight of the item just pick. The second item to pick is the most valuable item among those remaining. Keep follow the same strategy until thief cannot carry more item (due to weight).

Proof
  One way to proof the correctness of the above algorithm is to prove the greedy choice property and optimal substructure property. It consist of two steps. First, prove that there exists an optimal solution begins with the greedy choice given above. The second part prove that if A is an optimal solution to the original problem S, then A - a is also an optimal solution to the problem S - s where a is the item thief picked as in the greedy choice and S - s is the subproblem after the first greedy choice has been made. The second part is easy to prove since the more valuable items have less weight.
Note that if  v` / w` , is not it can replace any other because w` < w, but it increases the value because v` > v. □

Theorem     The fractional knapsack problem has the greedy-choice property.
Proof     Let the ratio v`/w` is maximal. This supposition implies that v`/w` ≥  v/w  for any pair (v, w), so v`v / w > v for any (v, w). Now Suppose a solution does not contain the full w` weight of the best ratio. Then by replacing an amount of any other w with more w` will improve the value. □

 

An Activity Selection Problem

 

An activity-selection is the problem of scheduling a resource among several competing activity.
 
Problem Statement   
Given a set S of n activities with and start time, S_i and f_i, finish time of an i^th activity. Find the maximum size set of mutually compatible activities.

Compatible Activities

Activities i and j are compatible if the half-open internal [s_i, f_i) and [s_j, f_j)
do not overlap, that is, i and j are compatible if s_i ≥ f_j  and s_j ≥  f_i

 

Greedy Algorithm for Selection Problem

I.     Sort the input activities by increasing finishing time.
        f₁ ≤  f₂ ≤  . . . ≤  f_n
II.    Call GREEDY-ACTIVITY-SELECTOR (s, f)

1. n = length [s]
2. A={i}
3. j = 1
4. for  i = 2  to  n
5.         do if   s_i ≥ f_j
6.              then  A= AU{i}
7.                       j = i
8. return  set A

Operation of the algorithm
Let 11 activities are given S = {p, q, r, s, t, u, v, w, x, y, z} start and finished times for proposed activities are (1, 4), (3, 5), (0, 6), 5, 7), (3, 8), 5, 9), (6, 10), (8, 11), (8, 12), (2, 13) and (12, 14).

A = {p} Initialization at line 2
A = {p, s} line 6 - 1^st iteration of FOR - loop
A = {p, s, w} line 6 -2^nd iteration of FOR - loop
A = {p, s, w, z} line 6 - 3^rd iteration of FOR-loop
Out of the FOR-loop and Return A = {p, s, w, z}

Analysis

Part I requires O(n lg n) time (use merge of heap sort).
Part II requires θ(n) time assuming that activities were already sorted in part I by their finish time.

Correctness
Note that Greedy algorithm do not always produce optimal solutions but GREEDY-ACTIVITY-SELECTOR does.

Theorem    Algorithm GREED-ACTIVITY-SELECTOR produces solution of maximum size for the activity-selection problem.

Proof Idea    Show the activity problem satisfied

1. Greedy choice property.
2. Optimal substructure property.

Proof

1. Let S = {1, 2, . . . , n} be the set of activities. Since activities are in order by finish time. It implies that activity 1 has the earliest finish time.
   Suppose, AS is an optimal solution and let activities in A are ordered by finish time. Suppose, the first activity in A is k.
   If k = 1, then A begins with greedy choice and we are done (or to be very precise, there is nothing to proof here).
   If k 1, we want to show that there is another solution B that begins with greedy choice, activity 1.
   Let B =  A - {k}{1}. Because f₁   f_k, the activities in B are disjoint and since B has same number of activities as A, i.e., |A| = |B|, B is also optimal.
2. Once the greedy choice is made, the problem reduces to finding an optimal solution for the problem. If A is an optimal solution to the original problem S, then A` = A - {1} is an optimal solution to the activity-selection problem S` = {i  S: S_i   f_i}. why? Because if we could find a solution B` to S` with more activities then A`, adding 1 to B` would yield a solution B to S with more activities than A, there by contradicting the optimality. □

As an example consider the example. Given a set of activities to among lecture halls. Schedule all the activities using minimal lecture halls.
In order to determine which activity should use which lecture hall, the algorithm uses the GREEDY-ACTIVITY-SELECTOR to calculate the activities in the first lecture hall. If there are some activities yet to be scheduled, a new lecture hall is selected and GREEDY-ACTIVITY-SELECTOR is called again. This continues until all activities have been scheduled.

LECTURE-HALL-ASSIGNMENT (s, f)

n = length [s)
for  i = 1 to n
        do HALL [i] = NIL
k = 1
while (Not empty (s))
        do HALL [k] = GREEDY-ACTIVITY-SELECTOR (s, t, n)
                k = k + 1
return HALL

Following changes can be made in the GREEDY-ACTIVITY-SELECTOR (s, f) (see CLR).

j = first (s)
A = i
for i = j + 1 to n
    do if s(i) not= "-"
            then if 

      GREED-ACTIVITY-SELECTOR (s, f, n)

j = first (s)
A = i = j + 1 to n
        if s(i] not = "-" then
            if s[i] ≥  f[j]|           
                then A = AU{i}
                            s[i] =  "-"
                                j = i
return A

Correctness 
The algorithm can be shown to be correct and optimal. As a contradiction, assume the number of lecture halls are not optimal, that is, the algorithm allocates more hall than necessary. Therefore, there exists a set of activities B which have been wrongly allocated. An activity b belonging to B which has been allocated to hall H[i] should have optimally been allocated to H[k]. This implies that the activities for lecture hall H[k] have not been allocated optimally, as the GREED-ACTIVITY-SELECTOR produces the optimal set of activities for a particular lecture hall.

Analysis
In the worst case, the number of lecture halls require is n. GREED-ACTIVITY-SELECTOR runs in θ(n). The running time of this algorithm is O(n²).
Two important Observations

• Choosing the activity of  least duration will not always produce an optimal solution. For example, we have a set of activities {(3, 5), (6, 8), (1, 4), (4, 7), (7, 10)}. Here, either (3, 5) or (6, 8) will be picked first, which will be picked first, which will prevent the optimal solution of {(1, 4), (4, 7), (7, 10)} from being found.
   
• Choosing the activity with the least overlap will not always produce solution. For example, we have a set of activities {(0, 4), (4, 6), (6, 10), (0, 1), (1, 5), (5, 9), (9, 10), (0, 3), (0, 2), (7, 10), (8, 10)}. Here the one with the least overlap with other activities is (4, 6), so it will be picked first. But that would prevent the optimal solution of  {(0, 1), (1, 5), (5, 9), (9, 10)} from being found.

 

An activity Selection Problem

An activity-selection is the problem of scheduling a resource among several competing activity.
Statement: Given a set S of n activities with and start time, S_i and f_i, finish time of an i^th activity. Find the maximum size set of mutually compatible activities.
Compatible Activities
Activities i and j are compatible if the half-open internal [s_i, f_i) and [s_j, f_j) do not overlap, that is, i and j are compatible if s_i ≥ f_j  and s_j ≥ f_i

Greedy Algorithm for Selection Problem

I. Sort the input activities by increasing finishing time.
f₁ ≤  f₂ ≤ . . . ≤  f_n
II Call GREEDY-ACTIVITY-SELECTOR (Sif)

1. n = length [s]
2. A={i}
3. j = 1
4. FOR i = 2 to n
5.         do if  s_i ≥ f_j
6.             then A= AU{i}
7.                     j = i
8. Return A

Operation of the algorithm
Let 11 activities are given S = {p, q, r, s, t, u, v, w, x, y, z} start and finished times for proposed activities are (1, 4), (3, 5), (0, 6), 5, 7), (3, 8), 5, 9), (6, 10), (8, 11), (8, 12), (2, 13) and (12, 14).

A = {p} Initialization at line 2
A = {p, s} line 6 - 1^st iteration of FOR - loop
A = {p, s, w} line 6 -2^nd iteration of FOR - loop
A = {p, s, w, z} line 6 - 3^rd iteration of FOR-loop
Out of the FOR-loop and Return A = {p, s, w, z}

Analysis
Part I requires O(nlgn) time (use merge of heap sort).
Part II requires Theta(n) time assuming that activities were already sorted in part I by their finish time.
CORRECTNESS
Note that Greedy algorithm do not always produce optimal solutions but GREEDY-ACTIVITY-SELECTOR does.
Theorem: Algorithm GREED-ACTIVITY-SELECTOR produces solution of maximum size for the activity-selection problem.
Proof Idea: Show the activity problem satisfied
I. Greedy choice property.
II. Optimal substructure property
Proof:
    I.  Let S = {1, 2, . . . , n} be the set of activities. Since activities are in order by finish time. It implies that activity 1 has the earliest finish time.
Suppose, A is a subset of S is an optimal solution and let activities in A are ordered by finish time. Suppose, the first activity in A is k.
If k = 1, then A begins with greedy choice and we are done (or to be very precise, there is nothing to proof here).
If k not=1, we want to show that there is another solution B that begins with greedy choice, activity 1.
Let B =  A - {k} U {1}. Because f₁ =< f_k, the activities in B are disjoint and since B has same number of activities as A, i.e., |A| = |B|, B is also optimal.
    II.  Once the greedy choice is made, the problem reduces to finding an optimal solution for the problem. If A is an optimal solution to the original problem S, then A` = A - {1} is an optimal solution to the activity-selection problem S` = {i in S: S_i >= f_i}.
why?
If we could find a solution B` to S` with more activities then A`, adding 1 to B` would yield a solution B to S with more activities than A, there by contradicting the optimality.



Problem: Given a set of activities to among lecture halls. Schedule all the activities using minimal lecture halls.
In order to determine which activity should use which lecture hall, the algorithm uses the GREEDY-ACTIVITY-SELECTOR to calculate the activities in the first lecture hall. If there are some activities yet to be scheduled, a new lecture hall is selected and GREEDY-ACTIVITY-SELECTOR is called again. This continues until all activities have been scheduled.
LECTURE-HALL-ASSIGNMENT (s,f)

n = length [s)
FOR i = 1 to n
        DO HALL [i] = NIL
k = 1
WHILE (Not empty (s))
        Do HALL [k] = GREEDY-ACTIVITY-SELECTOR (s, t, n)
                k = k + 1
RETURN HALL

Following changes can be made in the GREEDY-ACTIVITY-SELECTOR (s, f) (CLR).

j = first (s)
A = i
FOR i = j + 1 to n
    DO IF s(i) not= "-"
            THEN IF

GREED-ACTIVITY-SELECTOR (s,f,n)

j = first (s)
A = i = j + 1 to n
        IF s(i] not = "-" THEN
            IF s[i] >= f[j]|           
                THEN A = A U {i}
                            s[i] = "-"
                                j = i
return A

CORRECTNESS:
The algorithm can be shown to be correct and optimal. As a contradiction, assume the number of lecture halls are not optimal, that is, the algorithm allocates more hall than necessary. Therefore, there exists a set of activities B which have been wrongly allocated. An activity b belonging to B which has been allocated to hall H[i] should have optimally been allocated to H[k]. This implies that the activities for lecture hall H[k] have not been allocated optimally, as the GREED-ACTIVITY-SELECTOR produces the optimal set of activities for a particular lecture hall.
Analysis: 
In the worst case, the number of lecture halls require is n. GREED-ACTIVITY-SELECTOR runs in θ(n). The running time of this algorithm is O(n²).
Observe that choosing the activity of  least duration will not always produce an optimal solution. For example, we have a set of activities {(3, 5), (6, 8), (1, 4), (4, 7), (7, 10)}. Here, either (3, 5) or (6, 8) will be picked first, which will be picked first, which will prevent the optimal solution of {(1, 4), (4, 7), (7, 10)} from being found.
Also observe that choosing the activity with the least overlap will not always produce solution. For example, we have a set of activities {(0, 4), (4, 6), (6, 10), (0, 1), (1, 5), (5, 9), (9, 10), (0, 3), (0, 2), (7, 10), (8, 10)}. Here the one with the least overlap with other activities is (4, 6), so it will be picked first. But that would prevent the optimal solution of  {(0, 1), (1, 5), (5, 9), (9, 10)} from being found.

 

Huffman Codes

 

Huffman code is a technique for compressing  data. Huffman's greedy algorithm look at the occurrence of each character and it as a binary string in an optimal way.

Example
Suppose we have a data consists of 100,000 characters that we want to compress. The characters in the data occur with following frequencies.

	a	b	c	d	e	f
Frequency	45,000	13,000	12,000	16,000	9,000	5,000

Consider the problem of designing a "binary character code" in which each character is represented by a unique binary string.

Fixed Length Code
In fixed length code, needs 3 bits to represent six(6) characters.

	a	b	c	d	e	f
Frequency	45,000	13,000	12,000	16,000	9,000	5,000
Fixed Length code	000	001	010	011	100	101

This method require 3000,000 bits to code the entire file.
How do we get 3000,000?

• Total number of characters are 45,000 + 13,000 + 12,000 + 16,000 + 9,000 + 5,000 = 1000,000.
• Add each character is assigned 3-bit codeword => 3 * 1000,000 = 3000,000 bits.

Conclusion

Fixed-length code requires 300,000 bits while variable code requires 224,000 bits.
=> Saving of approximately 25%.

Prefix Codes
In which no codeword is a prefix of other codeword. The reason prefix codes are desirable is that they simply encoding (compression) and decoding.

Can we do better?
 
A variable-length code can do better by giving frequent characters short codewords and infrequent characters long codewords.

	a	b	c	d	e	f
Frequency	45,000	13,000	12,000	16,000	9,000	5,000
Fixed Length code	0	101	100	111	1101	1100

Character 'a' are 45,000
        each character 'a' assigned 1 bit codeword.
        1 * 45,000 = 45,000 bits.

Characters (b, c, d) are 13,000 + 12,000 + 16,000 = 41,000
        each character assigned 3 bit codeword
        3 * 41,000 = 123,000 bits

Characters (e, f) are 9,000 + 5,000 = 14,000
        each character assigned 4 bit codeword.
        4 * 14,000 = 56,000 bits.

Implies that the total bits are: 45,000 + 123,000 + 56,000 = 224,000 bits


Encoding:  Concatenate the codewords representing each characters of the file.

Example     From variable-length codes table, we code the3-character file abc as:

a	b	c
0	101	100	=> 0.101.100 = 0101100

Decoding 
Since no codeword is a prefix of other, the codeword that begins an encoded file is unambiguous.
To decode (Translate back to the original character), remove it from the encode file and repeatedly parse.
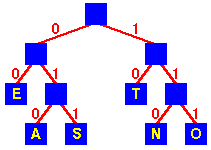
For example in "variable-length codeword" table, the string 001011101 parse uniquely as 0.0.101.1101, which is decode to aabe.
The representation of "decoding process" is binary tree, whose leaves are characters. We interpret the binary codeword for a character as path from the root to that character, where 0 means "go to the left child" and 1 means "go to the right child". Note that an optimal code for a file is always represented by a full (complete) binary tree.



Theorem     A Binary tree that is not full cannot correspond to an optimal prefix code.

Proof       Let T be a binary tree corresponds to prefix code such that T is not full. Then there must exist an internal node, say x, such that x has only one child, y. Construct another binary tree, T`, which has save leaves as T and have same depth as T except for the leaves which are in the subtree rooted at y in T. These leaves will have depth in T`, which implies T cannot correspond to an optimal prefix code.
To obtain T`, simply merge x and y into a single node, z is a child of parent of x (if a parent exists) and z is a parent to any children of y. Then T` has the desired properties: it corresponds to a code on the same alphabet as the code which are obtained, in the subtree rooted at y in T have depth in T` strictly less (by one) than their depth in T.
This completes the proof. □

	a	b	c	d	e	f
Frequency	45,000	13,000	12,000	16,000	9,000	5,000
Fixed Length code	000	001	010	011	100	101
Variable-length Code	0	101	100	111	1101	1100

Fixed-length code is not optimal since binary tree is not full.
Figure

Optimal prefix code because tree is full binary
Figure



From now on consider only full binary tree
If C is the alphabet from which characters are drawn, then the tree for an optimal prefix code has exactly |c| leaves (one for each letter) and exactly |c|-1 internal orders. Given a tree T corresponding to the prefix code, compute the number of bits required to encode a file. For each character c in C, let f(c) be the frequency of c and let d_T(c) denote the depth of c's leaf. Note that d_T(c) is also the length of codeword. The number of bits to encode a file is

B (T) = S f(c) d_T(c)

B (T) = S f(c) d_T(c)
         = 45*1 +13*3 + 12*3 + 16*3 + 9*4 +5*4
         = 224

Data Structure used: Priority queue = Q
Huffman (c)
n = |c|
Q = c
for  i =1  to   n-1
    do   z = Allocate-Node ()
             x = left[z] = EXTRACT_MIN(Q)
             y = right[z] = EXTRACT_MIN(Q)
            f[z] = f[x] + f[y]
            INSERT (Q, z)
return EXTRACT_MIN(Q)

Analysis

• Q implemented as a binary heap.
• line 2 can be performed by using BUILD-HEAP (P. 145; CLR) in O(n) time.
• FOR loop executed |n| - 1 times and since each heap operation requires O(lg n) time.
  => the FOR loop contributes (|n| - 1) O(lg n)
  => O(n lg n)
• Thus the total running time of Huffman on the set of n characters is O(nlg n).

 

 

Operation of the Algorithm

An optimal Huffman code for the following set of frequencies
        a:1    b:1    c:2    d:3    e:5    g:13    h:2
Note that the frequencies are based on Fibonacci numbers.
Since there are letters in the alphabet, the initial queue size is n = 8, and 7 merge steps are required to build the tree. The final tree represents the optimal prefix code.
Figure
The codeword for a letter is the sequence of the edge labels on the path from the root to the letter. Thus, the optimal Huffman code is as follows:

h :	1
g :	1	0
f :	1	1	0
e :	1	1	1	0
d :	1	1	1	1	0
c :	1	1	1	1	1	0
b :	1	1	1	1	1	1	0
a :	1	1	1	1	1	1	1

As we can see the tree is one long limb with leaves n=hanging off. This is true for Fibonacci weights in general, because the Fibonacci the recurrence is
       
To prove this, write F_j as F_j+1 - F_j-1 and sum from 0 to i, that is, F_-1 = 0.

 

Correctness of Huffman Code Algorithm

Proof Idea

Step 1: Show that this problem satisfies the greedy choice property, that is, if a greedy choice is made by Huffman's algorithm, an optimal solution remains possible.
Step 2: Show that this problem has an optimal substructure property, that is, an optimal solution to Huffman's algorithm contains optimal solution to subproblems.
Step 3: Conclude correctness of Huffman's algorithm using step 1 and step 2.

Lemma - Greedy Choice Property  Let c be an alphabet in which each character c has frequency f[c]. Let x and y be two characters in C having the lowest frequencies. Then there exists an optimal prefix code for C in which the codewords for x and y have the same length and differ only in the last bit.

Proof Idea   
 Take the tree T representing optimal prefix code and transform T into a tree T` representing another optimal prefix code such that the x characters x and y appear as sibling leaves of maximum depth in T`. If we can do this, then their codewords will have same length and differ only in the last bit.
Figures

Proof
  Let characters b and c are sibling leaves of maximum depth in tree T. Without loss of generality assume that f[b]  ≥  f[c] and f[x] ≤  f[y]. Since f[x] and f[y] are lowest leaf frequencies in order and f[b] and f[c] are arbitrary frequencies in order. We have f[x] ≤  f[b] and f[y] ≤  f[c]. As shown in the above figure, exchange the positions of leaves to get first T` and then T``. By formula, B(t) =  <sub>c in C</sub> f(c)d<sub>T</sub>(c), the difference in cost between T and T` is

B(T) - B(T`) = f[x]d<sub>T</sub>(x) + f(b)d<sub>T</sub>(b) - [f[x]d<sub>T</sub>(x) + f[b]d<sub>T`</sub>(b)
                    = (f[b] - f[x]) (d_T(b) - d_T(x))
                    = (non-negative)(non-negative)
                    ≥ 0

Two Important Points
The reason f[b] - f[x] is non-negative because x is a minimum frequency leaf in tree T and the reason d_T(b) - d_T(x) is non-negative that b is a leaf of maximum depth in T.
Similarly, exchanging y and c does not increase the cost which implies that B(T) - B(T`) ≥ 0. This fact in turn implies that B(T) ≤ B(T`), and since T is optimal by supposition, which implies  B(T`) = B(T). Therefore, T`` is optimal in which x and y are sibling leaves of maximum depth, from which greedy choice property follows.This complete the proof. □


Lemma - Optimal Substructure Property   Let T be a full binary tree representing an optimal prefix code over an alphabet C, where frequency f[c] is define for each character c belongs to set C. Consider any two characters x and y that appear as sibling leaves in the tree T and let z be their parent. Then, considering character z with frequency f[z] = f[x] + f[y], tree T` = T - {x, y} represents an optimal code for the alphabet C` = C - {x, y}U{z}.

Proof Idea
Figure

Proof
  We show that the cost B(T) of tree T can be expressed in terms of the cost B(T`). By considering the component costs in equation, B(T) =   f(c)d<sub>T</sub>(c), we show that the cost B(T) of tree T can be expressed in terms of the cost B(T`) of the tree T`. For each c belongs to C - {x, y}, we have d_T(c) = d_T(c)

  _cinC f[c]d_T(c) = S_cinC-{x,y} f[c]d_{T`</sub>(c)
                    = f[x](d<sub>T`} (z) + 1 + f[y] (d_{T`</sub>(z) +1)
                    = (f[x] + f[y]) d<sub>T`}(z) + f[x] + f[y]
And     B(T) = B(T`) + f(x) + f(y)

If T` is non-optimal prefix code for C`, then there exists a T`` whose leaves are the characters belongs to C` such that B(T``) < B(T`). Now, if x and y are added toT`` as a children of z, then we get a prefix code for alphabet C with cost B(T``) + f[x] + f[y] < B(T), Contradicting the optimality of T. Which implies that, treeT` must be optimal for the alphabet C. □



Theorem  Procedure HUFFMAN produces an optimal prefix code.

Proof
  Let S be the set of integers n ≥ 2 for which the Huffman procedure produces a tree of representing optimal prefix code for frequency f and alphabet C with |c| = n.
If C = {x, y}, then Huffman produces one of the following optimal trees.
figure
This clearly shows 2 is a member of  S. Next assume that n belongs to S and show that (n+1) also belong to S.
Let C is an alphabet with |c| = n + 1. By lemma 'greedy choice property', there exists an optimal code tree T for alphabet C. Without loss of generality, if x and y are characters with minimal frequencies then
    a. x and y are at maximal depth in tree T and b. and y have a common parent z.
Suppose that T` = T - {x,y} and C` = C - {x,y}U{z} then by lemma-optimal substructure property (step 2), tree T` is an optimal code tree for C`. Since |C`| = n and n belongs to S, the Huffman code procedure produces an optimal code tree T* for C`. Now let T** be the tree obtained from T* by attaching x and y as leaves to z.
Without loss of generality, T** is the tree constructed for C by the Huffman procedure. Now suppose Huffman selects a and b from alphabet C in first step so that f[a] not equal f[x] and f[b] = f[y]. Then tree C constructed by Huffman can be altered as in proof of lemma-greedy-choice-property to give equivalent tree with a and y siblings with maximum depth. Since T` and T* are both optimal for C`, implies that B(T`) = B(T*) and also B(T**) = B(T) why? because

B(T**) = B(T*) - f[z]d_T*(z) + [f[x] + f[y]] (d_T*(z) + 1)]
            = B(T*)  + f[x] + f[y]

Since tree T is optimal for alphabet C, so is T** . And T** is the tree constructed by the Huffman code.
And this completes the proof. □


Theorem     The total cost of a tree for a code can be computed as the sum, over all internal nodes, of the combined frequencies of the two children of the node.

Proof
Let tree be a full binary tree with n leaves. Apply induction hypothesis on the number of leaves in T. When n=2 (the case n=1 is trivially true), there are two leaves x and y (say) with the same parent z, then the cost of T is

B(T) = f(x)d_T(x) + f[y]d_T(y)
        = f[x] + f[y]                since d_T(x) = d_T(y) =1
        = f[child₁ of z] + f[child₂ of z].

Thus, the statement of theorem is true. Now suppose n>2 and also suppose that theorem is true for trees on n-1 leaves.
Let c₁ and c₂ are two sibling leaves in T such that they have the same parent p. Letting T` be the tree obtained by deleting c₁ and c₂, we know by induction that

B(T) =  _{leaves l` in T`} f[l`]d<sub>T</sub>(l`)
        =  _{internal nodes i` in T`} f[child₁of i`] + f [child<sub>2</sub> of  i`]

Using this information, calculates the cost of T.

B(T) =  _{leaves l in T} f[l]d_T(l)
        =  _{l not= c1, c2}  f[l]d_T(l) + f[c₁]d_T (c₁) -1) + f[c₂]d_T (c₂) -1) + f[c₁]+ f[c₂]
        =  _{leaves l` in T`} f[l]d<sub>T`</sub>(l) + f[c<sub>1</sub>]+ f[c<sub>2</sub>]
        =  <sub>internal nodes i` in T`</sub>  f[child<sub>1</sub>of i`] + f [child₂ of  i`] + f[c₁]+ f[c₂]
        =  _{internal nodes i in T} f[child₁of i] + f[child₁of i]

Thus the statement is true. And this completes the proof.

The question is whether Huffman's algorithm can be generalize to handle ternary codewords, that is codewords using the symbols 0,1 and 2. Restate the question, whether or not some generalized version of Huffman's algorithm yields optimal ternary codes? Basically, the algorithm is similar to the binary code example given in the CLR-text book. That is, pick up three nodes (not two) which have the least frequency and form a new node with frequency equal to the summation of these three frequencies. Then repeat the procedure. However, when the number of nodes is an even number, a full ternary tree is not possible. So take care of this by inserting a null node with zero frequency.

Correctness   
Proof is immediate from the greedy choice property and an optimal substructure property. In other words, the proof is similar to the correctness proof of Huffman's algorithm in the CLR.

 

Spanning Tree and

Minimum Spanning Tree

 

A spanning tree of a graph is any tree that includes every vertex in the graph. Little more formally, a spanning tree of a graph G is a subgraph of G that is a tree and contains all the vertices of G. An edge of a spanning tree is called a branch; an edge in the graph that is not in the spanning tree is called a chord. We construct spanning tree whenever we want to find a simple, cheap and yet efficient way to connect a set of terminals (computers, cites, factories, etc.). Spanning trees are important because of following reasons.

• Spanning trees construct a sparse sub graph that tells a lot about the original graph.
• Spanning trees a very important in designing efficient routing algorithms.
• Some hard problems (e.g., Steiner tree problem and traveling salesman problem) can be solved approximately by using spanning trees.
• Spanning trees have wide applications in many areas, such as network design, etc.

Greedy Spanning Tree Algorithm

One of the most elegant spanning tree algorithm that I know of is as follows:

• Examine the edges in graph in any arbitrary sequence.
• Decide whether each edge will be included in the spanning tree.

Note that each time a step of the algorithm is performed, one edge is examined. If there is only a finite number of edges in the graph, the algorithm must halt after a finite number of steps. Thus, the time complexity of this algorithm is clearly O(n), where n is the number of edges in the graph.

Some important facts about spanning trees are as follows:
 

• Any two vertices in a tree are connected by a unique path.
• Let T be a spanning tree of a graph G, and let e be an edge of G not in T. The T+e contains a unique cycle.

Lemma     The number of spanning trees in the complete graph K_n is n^n-2.


Greediness        It is easy to see that this algorithm has the property that each edge is examined at most once. Algorithms, like this one, which examine each entity at most once and decide its fate once and for all during that examination are called greedy algorithms. The obvious advantage of greedy approach is that we do not have to spend time reexamining entities.

Consider the problem of finding a spanning tree with the smallest possible weight or the largest possible weight, respectively called a minimum spanning tree and a maximum spanning tree. It is easy to see that if a graph possesses a spanning tree, it must have a minimum spanning tree and also a maximum spanning tree. These spanning trees can be constructed by performing the spanning tree algorithm (e.g., above mentioned algorithm) with an appropriate ordering of the edges.
Minimum Spanning Tree Algorithm
                    Perform the  spanning tree algorithm (above) by examining the edges is order of non decreasing weight (smallest first, largest last). If two or more edges have the same weight, order them arbitrarily.
Maximum Spanning Tree Algorithm
                    Perform the spanning tree algorithm (above) by examining the edges in order of non increasing weight (largest first, smallest last). If two or more edges have the same weight, order them arbitrarily.


A minimum spanning tree (MST) of a weighted graph G is a spanning tree of G whose edges sum  is minimum weight. In other words, a MST is a tree formed from a subset of the edges in a given undirected graph, with two properties:

• it spans the graph, i.e., it includes every vertex of the graph.
• it is a minimum, i.e., the total weight of all the edges is as low as possible.
  

Let G=(V, E) be a connected, undirected graph where V is a set of vertices (nodes) and E is the set of edges. Each edge has a given non negative length.
Problem    Find a subset T of the edges of G such that all the vertices remain connected when only the edges T are used, and the sum of the lengths of the edges in T is as small as possible.
Let G` = (V, T) be the partial graph formed by the vertices of G and the edges in T. [Note: A connected graph with n vertices must have at least n-1 edges AND more that n-1 edges implies at least one cycle]. So n-1 is the minimum number of edges in the T. Hence if G` is connected and T has more that n-1 edges, we can remove at least one of these edges without disconnecting (choose an edge that is part of cycle). This will decrease the total length of edges in T.
G` = (V, T) where T is a subset of E. Since connected graph of n nodes must have n-1 edges otherwise there exist at least one cycle. Hence if G` is connected and T has more that n-1 edges. Implies that it contains at least one cycle. Remove edge from T without disconnecting the G` (i.e., remove the edge that is part of the cycle). This will decrease the total length of the edges in T. Therefore, the new solution is preferable to the old one.
Thus, T with n vertices and more edges can be an optimal solution. It follow T must have n-1 edges and since G` is connected it must be a tree. The G` is called Minimum Spanning Tree (MST).

 

Prim's Algorithm

This algorithm was first propsed by Jarnik, but typically attributed to Prim. it starts from an arbitrary vertex (root) and at each stage, add a new branch (edge) to the tree already constructed; the algorithm halts when all the vertices in the graph have been reached. This strategy is greedy in the sense that at each step the partial spanning tree is augmented with an edge that is the smallest among all possible adjacent edges.
MST-PRIM
Input: A weighted, undirected graph G=(V, E, w)
Output: A minimum spanning tree T.
T={}
Let r be an arbitrarily chosen vertex from V.
U = {r}
WHILE | U| < n
DO
Find u in U and v in V-U such that the edge (u, v) is a smallest edge between U-V.
T = TU{(u, v)}
U= UU{v}
Analysis
The algorithm spends most of its time in finding the smallest edge. So, time of the algorithm basically depends on how  do we search this edge.
Straightforward method
Just find the smallest edge by searching the adjacency list of the vertices in V. In this case, each iteration costs O(m) time, yielding a total running time of O(mn).
Binary heap
By using binary heaps, the algorithm runs in O(m log n).
Fibonacci heap
By using Fibonacci heaps, the algorithm runs in O(m + n log n) time.

 

Dijkstra's Algorithm (Shortest Path)

 

Consider a directed graph G = (V, E).
Problem    Determine the length of the shortest path from the source to each of the other nodes of the graph. This problem can be solved by a greedy algorithm often called Dijkstra's algorithm.
The algorithm maintains two sets of vertices, S and C. At every stage the set S contains those vertices that have already been selected and set C contains all the other vertices. Hence we have the invariant property V=S U C. When algorithm starts Delta contains only the source vertex and when the algorithm halts, Delta contains all the vertices of the graph and problem is solved. At each step algorithm choose the vertex in C whose distance to the source is least and add it to S.