 Automaton
AutomatonIn theoretical computer science, automata theory is the study of abstract machines (or more appropriately, abstract 'mathematical' machines or systems) and the computational problems that can be solved using these machines. These abstract machines are called automata.
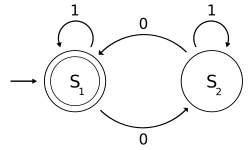
The figure at right illustrates a finite state machine, which is one well-known variety of automaton. This automaton consists of states (represented in the figure by circles), and transitions (represented by arrows). As the automaton sees a symbol of input, it makes atransition (or jump) to another state, according to its transition function (which takes the current state and the recent symbol as its inputs).
Automata theory is also closely related to formal language theory, as the automata are often classified by the class of formal languagesthey are able to recognize. An automaton can be a finite representation of a formal language that may be an infinite set.
- Introduction (PDF)
- Mathematical Concepts (PDF)
- Formal Languages (PDF)
- Context Free Grammars (PDF)
- Parsing (PDF)
- Normal Forms (PDF)
- Automata (PDF)
- Deterministic Finite Automata (PDF)
- Nondeterministic Finite Automata (PDF)
- Regular and Nonregular Languages (PDF)
- Pushdown Automata (PDF)
- Deterministic Parsing: LL(k) Grammars (PDF)
- Turing Machines (PDF)
- Wrapup (PDF)
Variations in definition of automata
Automata are defined to study useful machines under mathematical formalism. So, the definition of an automaton is open to variations according to the "real world machine", which we want to model using the automaton. People have studied many variations of automata. Above, the most standard variant is described, which is called deterministic finite automaton. The following are some popular variations in the definition of different components of automata.
- Input
- Finite input: An automaton that accepts only finite sequence of words. The above introductory definition only accepts finite words.
- Infinite input: An automaton that accepts infinite words (ω-words). Such automata are called ω-automata.
- Tree word input: The input may be a tree of symbols instead of sequence of symbols. In this case after reading each symbol, the automaton reads all the successor symbols in the input tree. It is said that the automaton makes one copy of itself for each successor and each such copy starts running on one of the successor symbol from the state according to the transition relation of the automaton. Such an automaton is called tree automaton.
- States
- Finite states: An automaton that contains only a finite number of states. The above introductory definition describes automata with finite numbers of states.
- Infinite states: An automaton that may not have a finite number of states, or even a countable number of states. For example, the quantum finite automaton or topological automatonhas uncountable infinity of states.
- Stack memory: An automaton may also contain some extra memory in the form of a stack in which symbols can be pushed and popped. This kind of automaton is called a pushdown automaton
- Transition function
- Deterministic: For a given current state and an input symbol, if an automaton can only jump to one and only one state then it is a deterministic automaton.
- Nondeterministic: An automaton that, after reading an input symbol, may jump into any of a number of states, as licensed by its transition relation. Notice that the term transition function is replaced by transition relation: The automaton non-deterministically decides to jump into one of the allowed choices. Such automaton are called nondeterministic automaton.
- Alternation: This idea is quite similar to tree automaton, but orthogonal. The automaton may run its multiple copies on the same next read symbol. Such automata are calledalternating automaton. Acceptance condition must satisfy all runs of such copies to accept the input.
- Acceptance condition
- Acceptance of finite words: Same as described in the informal definition above.
- Acceptance of infinite words: an omega automaton cannot have final states, as infinite words never terminate. Rather, acceptance of the word is decided by looking at the infinite sequence of visited states during the run.
- Probabilistic acceptance: An automaton need not strictly accept or reject an input. It may accept the input with some probability between zero and one. For example, quantum finite automaton, geometric automaton and metric automaton has probabilistic acceptance.
