- Aggregate Method
- Accounting Method
- Potential Method
- Dynamic Table
Amortized Analysis
In an amortized analysis, the time required to perform a sequence of data structure operations is average over all operation performed. Amortized analysis can be used to show that average cost of an operation is small, if one average over a sequence of operations, even though a single operation might be expensive. Unlike the average probability distribution function, the amortized analysis guarantees the 'average' performance of each operation in the worst case.
CLR covers the three most common techniques used in amortized analysis. The main difference is the way the cost is assign.
- Aggregate Method
- Computes an upper bound T(n) on the total cost of a sequence of n operations.
- Accounting Method
- Overcharge some operations early in the sequence. This 'overcharge' is used later in the sequence for pay operation that charges less than they actually cost.
- Potential Method
- Maintain the credit as the potential energy to pay for future operations.
Aggregate Method
Aggregate Method Characteristics
- It computes the worst case time T(n) for a sequence of n operations.
- The amortized cost is T(n)/n per operation.
- It gives the average performance of each operation in the worst case.
- This method is less precise than other methods, as all operations are assigned the same cost.
Application 1: Stack operations
In the following pseudocode, the operation STACK-EMPTY returns TRUE if there are no object currently on the stack, and FALSE otherwise.
MULTIPOP(s, k)
while (.NOT. STACK-EMPTY(s) and k ≠ 0)
do pop(s)
k = k-1
while (.NOT. STACK-EMPTY(s) and k ≠ 0)
do pop(s)
k = k-1
Analysis
- Worst-case cost for MULTIPOP is O(n). There are n successive calls to MULTIPOP would cost O(n2). We get unfair cost O(n2) because each item can be poped only once for each time it is pushed.
- In a sequence of n mixed operations the most times multipop can be called n/2.Since the cost of push and pop is O(1), the cost of n stack operations is O(n). Therefore, amortized cost of an operation is the average: O(n)/n = O(1).
Application 2: Binary Counter
We use an array A[0 . . k-1] of bits, where length [A] = k, as the counter. A binary number x that is stored in the counter has its lowest-order bit in A[0] and its highest-order bit is A[k-1], so that k-1Si=0 2iA[i]. Initially, x = 0, and thus A[i] = 0 for i=0, 1, . . . , k-1.
To add 1 (modulus 2k ) to the value in the counter, use the following pseudocode.
INCREMENT (A)
i = 0
while i < length [A] and A[i] = 1
do A[i] = 0
i = i+1
if i < length [A]
then A[i] = 1
i = 0
while i < length [A] and A[i] = 1
do A[i] = 0
i = i+1
if i < length [A]
then A[i] = 1
A single execution of INCREMENT takes O(k) in worst case when Array A contains all 1's. Thus, a sequence of n INCREMENT operation on an initially zero counter takes O(nk) in the worst case. This bound is correct but not tight.
Amortized Analysis
We can tighten the analysis to get a worst-case cost for a sequence of an INCREMENT's by observing that not all bits flip each time INCREMENT is called.In general, for i = 0, 1, . . .,Bit A[0] is changed ceiling n times (every time)
Bit A[0] is changed ceiling [n/21] times (every other time)
Bit A[0] is changed ceiling [n/22] times (every other time)
.
.
.
Bit A[0] is changed ceiling [n/2i] times.
 lg n
lg n , bit A[i] flips
, bit A[i] flips  n/2i
n/2i times in a sequence of n INCREMENT operations on an initially zero counter.
times in a sequence of n INCREMENT operations on an initially zero counter.For i >
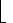 lg(n)
lg(n)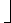 , bit A
, bit A  i
i never flips at all. The total number of flips in a sequence is thus
never flips at all. The total number of flips in a sequence is thusfloor(log)Si=0
 n/2i
n/2i < n ∞Si=0 1/2i = 2n
< n ∞Si=0 1/2i = 2nTherefore, the worst-case time for a sequence of n INCREMENT operation on an initially zero counter is therefore O(n), so the amortized cost of each operation is O(n)/n =O(1).
Accounting Method
In this method, we assign changes to different operations, with some operations charged more or less than they actually cost. In other words, we assign artificial charges to different operations.
- Any overcharge for an operation on an item is stored (in an bank account) reserved for that item.
- Later, a different operation on that item can pay for its cost with the credit for that item.
- The balanced in the (bank) account is not allowed to become negative.
- The sum of the amortized cost for any sequence of operations is an upper bound for the actual total cost of these operations.
- The amortized cost of each operation must be chosen wisely in order to pay for each operation at or before the cost is incurred.
Application 1: Stack Operation
Recall the actual costs of stack operations were:
PUSH (s, x) 1
POP (s) 1
MULTIPOP (s, k) min(k,s)
POP (s) 1
MULTIPOP (s, k) min(k,s)
The amortized cost assignments are
PUSH 2
POP 0
MULTIPOP 0
Observe that the amortized cost of each operation is O(1). We must show that one can pay for any sequence of stack operations by charging the amortized costs.
The two units costs collected for each PUSH is used as follows:
- 1 unit is used to pay the cost of the PUSH.
- 1 unit is collected in advanced to pay for a potential future POP.
Therefore, for any sequence for n PUSH, POP, and MULTIPOP operations, the amortized cost is an
Ci = j=1Si 3 - Ciactual = 3i - (2floor(lg1) + 1 + i -floor(lgi) - 2)This is an upperbound on the total actual cost. Since the total amortized cost is O(n) so is the total cost.
If i = 2k, where k ≥ 0, then
Ci = 3i - (2k+1 + i - k -2)
= k + 2
If i = 2k + j, where k ≥ 0 and 1 ≤ j ≤ 2k, then
Ci = 3i - (2k+1 + i - k - 2)
= 2j + k + 2
As an example, consider a sequence of n operations is performed on a data structure. The ith operation costs i if i is an exact power of 2, and 1 otherwise. The accounting method of amortized analysis determine the amortized cost per operation as follows:
Let amortized cost per operation be 3, then the credit Ci after the ith operation is: Since k ≥ 1 and j ≥ 1, so credit Ci always greater than zero. Hence, the total amortized cost 3n, that is O(n) is an upper bound on the total actual cost. Therefore, the amortized cost of each operation is O(n)/n = O(1).
Another example, consider a sequence of stack operations on a stack whose size never exceeds k. After every k operations, a copy of the entire stack is made. We must show that the cost of n stack operations, including copying the stack, is O(n) by assigning suitable amortized costs to the various stack operations.
There are, ofcourse, many ways to assign amortized cost to stack operations. One way is:
PUSH 4,Every time we PUSH, we pay a dollar (unit) to perform the actual operation and store 1 dollar (put in the bank). That leaves us with 2 dollars, which is placed on x (say) element. When we POP x element off the stack, one of two dollar is used to pay POP operation and the other one (dollar) is again put into a bank account. The money in the bank is used to pay for the STACK-COPY operation. Since after kk dollars in the bank and the stack size is never exceeds k, there is enough dollars (units) in the bank (storage) to pay for the STACK-COPY operations. The cost of n stack operations, including copy the stack is therefore O(n). operations, there are atleast
POP 0,
MULTIPOP 0,
STACK-COPY 0.
Application 2: Binary Counter
We observed in the method, the running time of INCREMENT operation on binary counter is proportion to the number of bits flipped. We shall use this running time as our cost here.
For amortized analysis, charge an amortized cost of 2 dollars to set a bit to 1.
When a bit is set, use 1 dollar out of 2 dollars already charged to pay the actual setting of the bit, and place the other dollar on the bit as credit so that when we reset a bit to zero, we need not charge anything.
The amortized cost of psuedocode INCREMENT can now be evaluated:
INCREMENT (A)
1. i = 0
2. while i < length[A] and A[i] = 1
3. do A[i] = 0
4. i = i +1
5. if i < length [A]
6. then A[i] = 1
Within the while loop, the cost of resetting the bits is paid for by the dollars on the bits that are reset.At most one bit is set, in line 6 above, and therefore the amortized cost of an INCREMENT operation is at most 2 dollars (units). Thus, for n INCREMENT operation, the total amortized cost is O(n), which bounds the total actual cost.
Consider a Variant
Let us implement a binary counter as a bit vector so that any sequence of n INCREMENT and RESET operations takes O(n) time on an initially zero counter,. The goal here is not only to increment a counter but also to read it to zero, that is, make all bits in the binary counter to zero. The new field , max[A], holds the index of the high-order1 in A. Initially, set max[A] to -1. Now, update max[A] appropriately when the counter is incremented (or reset). By contrast the cost of RESET, we can limit it to an amount that can be covered from earlier INCREMENT'S.
INCREMENT (A)
1. i = 1
2. while i < length [A] and A[i] = 1
3. do A[i] = 0
4. i = i +1
5. if i < length [A]
6. then A[i] = 1
7. if i > max[A]
8. then max[A] = i
9. else max[A] = -1
Note that lines 7, 8 and 9 are added in the CLR algorithm of binary counter.
RESET(A)
For i = 0 to max[A]
do A[i] = 0
max[A] = -1
For the counter in the CLR we assume that it cost 1 dollar to flip a bit. In addition to that we assume that we need 1 dollar to update max[A]. Setting and Resetting of bits work exactly as the binary counter in CLR: Pay 1 dollar to set bit to 1 and placed another 1 dollar on the same bit as credit. So, that the credit on each bit will pay to reset the bit during incrementing.
In addition, use 1 dollar to update max[A] and if max[A] increases place 1 dollar as a credit on a new high-order 1. (If max[A] does not increase we just waste that one dollar). Since RESET manipulates bits at some time before the high-order 1 got up to max[A], every bit seen by RESET has one dollar credit on it. So, the zeroing of bits by RESET can be completely paid for by the credit stored on the bits. We just need one dollar to pay for resetting max[A].
Thus, charging 4 dollars for each INCREMENT and 1 dollar for each RESET is sufficient, so the sequence of n INCREMENT and RESET operations take O(n) amortized time.
Potential Method
This method stores pre-payments as potential or potential energy that can be released to pay for future operations. The stored potential is associated with the entire data structure rather than specific objects within the data structure.
Notation:
- D0 is the initial data structure (e.g., stack)
- Di is the data structure after the ith operation.
- ci is the actual cost of the ith operation.
- The potential function Ψ maps each Di to its potential value Ψ(Di)
The amortized cost of each operation is therefore^ci = ci + Ψ(Di) - Ψ (Di-1) --------- (1)
By the eq.I, the total amortized cost of the n operation is^ci = [Actual operation cost] + [change in potential].
ni=1 ^ci = n
i=1(ci + Ψ(Di) - Ψ (Di-1) )
= ni=1 ci + n
i=1 Ψ(Di) - n
i=1Ψ (Di-1)
= ni=1 ci + Ψ(D1) + Ψ(D2) + . . . + Ψ (Dn-1) + Ψ(Dn) - {Ψ(D0) + Ψ(D1) + . . . + Ψ (Dn-1)
= ni=1 ci + Ψ(Dn) - Ψ(D0) ----------- (2)
If we define a potential function Ψ so that Ψ(Dn) ≥ Ψ(D0), then the total amortized cost n
As an example consider a sequence of n operations performed on a data structure. The ith operation costs i if i is an exact power of 2 and 1 otherwise. The potential method of amortized determines the amortized cost per operation as follows:
Let Ψ(Di) = 2i - 2ëlgi+1û + 1, then
Ψ(D0) = 0. Since 2ëlgi+1û ≤ 2i where i >0 ,
Therefore, Ψ(Di) ≥ 0 = Ψ(D0)
If i = 2k where k ≥ 0 then
2ëlgi+1û = 2k+1 = 2i
2ëlgiû = 2k = i
^ci = ci + Ψ(Di) - Ψ(Di-1)
= i + (2i -2i+1) -{2(i-1)-i+1}
= 2
If i = 2k + j where k ≥ 0 and 1 ≤ j ≤ 2kthen 2ëlgi+1û = 2[lgi]Because n
^ci = ci + Ψ(Di) - Ψ(Di-1) = 3
and Ψ(Di) ≥ Ψ(D0), so, the total amortized cost of n operation is an upper bound on the total actual cost. Therefore, the total amortized cost of a sequence of noperation is O(n) and the amortized cost per operation is O(n) / n = O(1).
Application 1- Stack Operations
Define the potential function Ψ on a stack to be the number of objects in the stack. For empty stack D0 , we have Ψ(D0) = 0. Since the number of objects in the stack can not be negative, the stack Di after the ith operation has nonnegative potential, and thus
Ψ(Di) ≥ 0 = Ψ(D0).
Therefore, the total amortized cost of n operations w.r.t. function Ψ represents an upper bound on the actual cost.
Amortized costs of stack operations are:
PUSH
If the ith operation on a stack containing s object is a PUSH operation, then the potential difference is
Ψ(Di) - Ψ(Di-1) = (s + 1) - s = 1In simple words, if ith is PUSH then (i-1)th must be one less. By equation I, the amortized cost of this PUSH operation is
^ci = ci + Ψ(Di) - Ψ(Di-1) = 1 + 1 = 2
MULTIPOP
If the ith operation on the stack is MULTIPOP(S, k) and k` = min(k,s) objects are popped off the stack.
The actual cost of the operation is k`, and the potential difference is
why this is negative? Because we are taking off item from the stack. Thus, the amortized cost of the MULTIPOP operation isΨ(Di) - Ψ(Di-1) = -k`
^ci = ci + Ψ(Di) - Ψ(Di-1) = k`-k` = 0
POP
Similarly, the amortized cost of a POP operation is 0.
Analysis
Since amortized cost of each of the three operations is O(1), therefore, the total amortized cost of n operations is O(n). The total amortized cost of n operations is an upper bound on the total actual cost.
Lemma If data structure is Binary heap: Show that a potential function is O(nlgn) such that the amortized cost of EXTRACT-MIN is constant.
Proof
We know that the amortized cost ^ci of operation i is defined as
For the heap operations, this gives us
^ci = ci + Ψ(Di) - Ψ(Di-1)
c1lgn = c2lg(n+c3) + Ψ(Di) - Ψ(Di-1) (Insert) ------------(1)
c4 = c5lg(n + c6) + Ψ(Di) - Ψ(Di-1) (EXTRACT-MIN) -----(2)
Consider the potential function Ψ(D) = lg(n!), where n is the number of items in D.
Remember that stirlings function tells that lg(n!) = θ(nlgn), soFrom equation (1), we have
From equation (2), we have(c1 - c2)lg(n + c3) = lg(n!) - lg ((n-1)!) = lgn.
This clearly holds if c1 = c2 and c3 = 0.
c4 - c5 lg(n + c6) = lg(n!) - lg ((n+1)!) = - lg(n+1).
This clearly holds if c4 = 0 and c4 = c6 = 1.
And this completes the proof.Ψ(D) = θ(n lg n)
Application 2: Binary Counter
Define the potential of the counter after ith INCREMENT operation to be bi, the number of 1's in the counter after ith operation.
Let ith INCREMENT operation resets ti bits. This implies that actual cost = atmost (ti + 1).
Why? Because in addition to resetting ti it also sets at most one bit to 1.
Therefore, the number of 1's in the counter after the ith operation is therefore bi ≤ bi-1 - ti + 1, and the potential difference is
Ψ(Di) - Ψ(Di-1) ≤ (bi-1 - ti + 1) - bi-1 = 1- ti
Putting this value in equation (1), we get
If counter starts at zero, then Ψ(D0) = 0. Since Ψ(Di) ≥ 0 for all i, the total amortized cost of a sequence of n INCREMENT operation is an upper bound on the total actual cost, and so the worst-case cost of n INCREMENT operations is O(n).^ci = ci + Ψ(Di) - Ψ (Di-1)
= (ti + 1) + (1- ti)
= 2
If counter does not start at zero, then the initial number are 1's (= b0).
After 'n' INCREMENT operations the number of 1's = bn, where 0 ≤ b0, bn ≤ k.
Since ni=1^ci = (ci + Ψ(Di) + Ψ(Di-1))
=> ni=1^ci = n
i=1 ci + n
i=1 Ψ(Di) + n
i=1 Ψ(Di-1)
=> ni=1^ci = nSi=1 ci + Ψ(Dn) - Ψ(D0)
=> ni=1ci = n
i=1 ^ci + Ψ(D0) - Ψ(Dn)
We have ^ci ≤ 2 for all 1≤ i ≤ n. Since Ψ(Di) = b0 and Ψ(Dn) = b, the total cost of n INCREMENT operation is
Since ni=1ci = n
i=1 ^ci + Ψ(Dn) + Ψ(D0)
≤ n
i=1 2 - bn + b0 why because ci ≤ 2
= 2 n
i=1 - bn + b0
= 2n - bn + b
Note that since b0 ≤ k, if we execute at least n = Ω(k) INCREMENT Operations, the total actual cost is O(n), no matter what initial value of counter is.
Implementation of a queue with two stacks, such that the amortized cost of each ENQUEUE and each DEQUEUE Operation is O(1). ENQUEUE pushes an object onto the first stack. DEQUEUE pops off an object from second stack if it is not empty. If second stack is empty, DEQUEUE transfers all objects from the first stack to the second stack to the second stack and then pops off the first object. The goal is to show that this implementation has an O(1) amortized cost for each ENQUEUE and DEQUEUE operation. Suppose Di denotes the state of the stacks after ith operation. Define Ψ(Di) to be the number of elements in the first stack. Clearly, Ψ(D0) = 0 and Ψ(Di) ≥ Ψ(D0) for all i. If the ith operation is an ENQUEUE operation, then Ψ(Di) - Ψ(Di-1) = 1
Since the actual cost of an ENQUEUE operation is 1, the amortized cost of an ENQUEUE operation is 2. If the ith operation is a DEQUEUE, then there are two case to consider.
- Case i: When the second stack is not empty.
- In this case we have Ψ(Di) - Ψ(Di-1) = 0 and the actual cost of the DEQUEUE operation is 1.
- Case ii: When the second stack is empty.
- In this case, we have Ψ(Di) - Ψ(Di-1) = - Ψ(Di-1) and the actual cost of the DEQUEUE operation is Ψ(Di-1) + 1 .
In either case, the amortize cost of the DEQUEUE operation is 1. It follows that each operation has O(1) amortized cost
Dynamic Table
If the allocated space for the table is not enough, we must copy the table into larger size table. Similarly, if large number of members erased from the table, it is good idea to reallocate the table with a smaller size. Using amortized analysis we shall show that the amortized cost of insertion and deletion is constant and unused space in a dynamic table never exceeds a constant fraction of the total space.
Assume that the dynamic table supports following two operations:
- TABLE-INSERT
This operation add an item in the table by copying into the unused single slot. The cost of insertion is 1.
- TABLE-DELETE
This operation removes an item from the table by freeing a slot. The cost of deletion is 1.
Load Factor
The number of items stored in the table, n, divided by the size of the table, m, is defined as the load factor and denoted as T(α) = m/nThe load factor of the empty table (size m=0) is 1.
A table is full when there exists no used slots. That is, the number of items stored in the table equals the number of available slots (m=n). In this case
Load factor 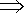 T(α) = n/m = 1
T(α) = n/m = 1
Proposed Algorithm
- Initialize table size to m=1.
- Keep inserting elements as long as size of the table less than number of items i.e., n<m.
- Generate a new table of size 2m and set m <-- 2m.
- Copy items (by using elementary insertion) from the old table into the new one.
- GOTO step 2.
Analysis
If n elementary insert operations are performed in line 4, the worst-case cost of an operation is O(n), which leads to an upper bound of O(n2) on the total running time for noperations.Aggregate Analysis
The ith insert operation causes an expansion only when i - 1 an exact power of 2. Let ci be the cost of the ith insert operation. Then
ci = i if i - 1 is an exact power of 2
1 Otherwise
As an example, consider the following illustration.
INSERTION TABLE-SIZE COST n
m 1 1 1 1+1 2 2 1+2 3 4 1 4 4 1+4 5 8 1 6 8 1 7 8 1 8 8 1 9 16 1+8 10 16 1
The total cost of n insert operations is therefore
Therefore, the amortized cost of a single operation isn∑i=1 ci ≤ n + floor(lgn)∑j=0 2j
= n + [2floor(lgn)+1 -1]/[2-1] since n∑k=0 xk = [xn+1 -1]/[x-1]
= n + 2lgn . 2-1
= n + 2n - 1
= 3n - 1
< 3n
Asymptotically, the cost of dynamic table is O(1) which is the same as that of table of fixed size.= Total cost Number of operations
= 3n/n
= 3
Accounting Method
Here we guess charges to 3$. Intuitively, each item pays for 3 elementary operations.- 1$ for inserting immediate item.
- 1$ for moving item (re-insert) when the table is expanded.
- 1$ for moving another item (re-insert) has already been moved once when that table is expanded.
Potential Method
Define a potential function Φ that is 0 immediately after an expansion but potential builds to the table size by the time the table is full.Φ(T) = 2 . num[T] - size[T]
Immediately after an expansion (but before any insertion) we have, num[T] = size[T]/2
which implies
Immediately before an expansion, we have num[T] = size[T],Φ(T) = 2 . num[T] - 2 num[T]
= 0
which implies
The initial value of the potential function is zero i.e., Φ(T) = 0, and half-full i.e., num[T] ≥ size[T]/2. or 2 num[T] ≥ size[T]Φ(T) = 2 . num[T] - num[T]
= num[T]
which implies
Φ(T) = 2 num[T] - size[T] ≥ 0
That is, Φ(T) is always nonnegative.Before, analyze the amortized cost of the ith TABLE-INSERT operation define following.
Let
numi = number of elements in the table after ith operation
sizei = table after ith operation.
Φi = Potential function after ith operation.
Initially, we have num0 = size0 =0 and Φ0 = 0.
If ith insertion does not trigger an expansion, then sizei = sizei-1 and the amortized cost of the operation is
^ci = ci + Φi - Φi-1
= 1 + [2 . numi - sizei] - [2 . numi-1- sizei-1]
= 1 + 2 numi - sizei - 2(numi- 1) - sizei
= 1 + 2numi - sizei - 2numi + 2 - sizei
= 3
If the ith insertion does trigger an expansion, then (size of the table becomes double) then sizei = sizei-1 = numi and the amortized cost of the operation is 2
^ci = ci + Φi - Φi-1
= numi + [2 . numi - sizei] - [2 . numi-1 - sizei-1]
= numi + 2numi - sizei - 2 . numi-1 + sizei-1
= numi + 2numi -2(numi -1) -2(numi -1) + (numi -1)
= numi +2numi-2numi-2 -2numi + 2 + numi -1
= 4 -1
= 3
What is the catch? It show how potential builds (from zero) to pay the table expansion.
Dynamic Table Expansion and Contraction
When the load factor of the table, α(T) = n/m, becomes too small, we want to preserve following two properties:- Keep the load factor of the dynamic table below by a constant.
- Keep the amortized cost of the dynamic table bounded above by a constant.
Proposed Strategy
Even: When an item is inserted into full table.The problem with this strategy is trashing. We can avoid this problem by allowing the load factor of the table, α(T) = n/m, to drop below 1/2 before contradicting it. By contradicting the table when load factor falls below 1/4, we maintain the lower bound α(T) ≥ 1/4 i.e., load factor is bounded by the constant 1/4.
Action: Double the size of the table i.e., m ← 2m.
Even: When removing of an item makes table less the half table.
Action: Halve the size of the table i.e., m ← m/2.
Load Factor
The load factor α(T), of non-empty table T is defined as the number of items stored in the T divided by the size of T, which is number slots in T, i.e., α(T) = num[T] / size[T]
Since for an empty table, we have
num[T] = size[T] = 0 and α(T) = 1
which implies that we always have
num[T] = α(T) . size[T]
whether table is empty or not.Analysis by Potential Method
We start by defining a potential function Φ that is- 0 immediately after an expansion and builds as the load factor, α(T) = n/m, increases to 1.
- 0 immediately after a contraction and builds as the load factor, α(T) = n/m, decreases to 1/4.
Note that the potential function is never negative.
Φ(T) 2 . num[T] - size(T) if α(T) ≥ 1/2 size(T) - num[T] if α(T) < 1/2
Properties of Potential Function
When α(T) = 1/2α(T) = num[T] = 1/2
size[T]
implies that size[T] = 2 num[T]
And the potential function is
since Φ(T) = 2 num[T] - size[T]When α(T) = 1
= 2 num[T] - 2 num[T]
= 0
since α(T) = num[T] = 1
size[T]
implies that size[T] = num[T]
And the potential function is
since Φ(T) = 2 num[T] - size[T]which indicates that the potential can pay for an expansion if an item is inserted.
= 2 num[T] - num[T]
= num[T]
When α(T) = 1/4, then
since α(T) = num[T] = 1/4
size[T]
implies that size[T] = 4 num[T]
And the potential function is
Φ(T) = size[T]/2 - num[T]which indicates that the potential can pay for a contradiction if an item is deleted.
= 4 num[T]/2 - num[T]
= num[T]
Notation
The subscript is used in the existing notations to denote their values after the ith operations. That is to say, ^ci, ci, numi, sizei, αi and Φi indicate values after the ith operation.Initially
num0 = size0 = Φ0 = 1 and α0



0 comments